Discrete and Computational Geometry 44, 245 (2010); arXiv:0910.5226
We present a one-parameter family of periodic packings of regular tetrahedra, with the packing fraction 100/117≈0.8547, that are simple in the sense that they are transitive and their repeating units involve only four tetrahedra. The construction of the packings was inspired from results of a numerical search that yielded a similar packing. We present an analytic construction of the packings and a description of their properties. We also present a transitive packing with a repeating unit of two tetrahedra and a packing fraction (139+40√10)/369≈0.7194.
The optimization problem of packing regular tetrahedra densely in space has seen invigorated interest over the last few years [CT06, Chen08, TY09a, TY09b, HEK09]. This interest has helped drive up the packing fraction of the densest-known such packings from $0.7174$ in 2006 [CT06] to $0.8503$ [HEK09] most recently (see Table 3). These improved packing fractions have been obtained from more and more complex packings, with larger and larger repeating units. This trend has led some to conjecture that the densest packing of tetrahedra might have inherent disorder [TY09b]. The more restrictive problem of packing tetrahedra transitively --- that is, so that all tetrahedra in the packing are equivalent (a more rigorous definition is given below) --- has been less extensively studied and the densest previously-reported transitive packing of regular tetrahedra fills only $2/3$ of space [CT06]. Here we present a one-parameter family of transitive but dense packings of tetrahedra with the packing fraction $100/117\approx0.8547$.
The discovery of this family of dense packings was inspired by the results of a numerical search, which yielded a dense packing with similar structural properties to the packing we present. The numerical method used was adapted from the divide and concur approach to constraint satisfaction problems [GE08]. The divide and concur formalism enables us to set up an efficient search through the parameter space consisting of the positions and orientations of tetrahedra inside the repeating unit and the translation vectors governing its lattice repetition, subject to the constraint that no two tetrahedra overlap. The dynamics involved in the divide and concur search are highly non-physical, which might explain why our method was able to discover this dense packing, while earlier methods involving more physical dynamics were not [TY09a,TY09b,HEK09]. In this note we present only the analytically constructed packing without a full explication of the numerical method, which will be forthcoming.
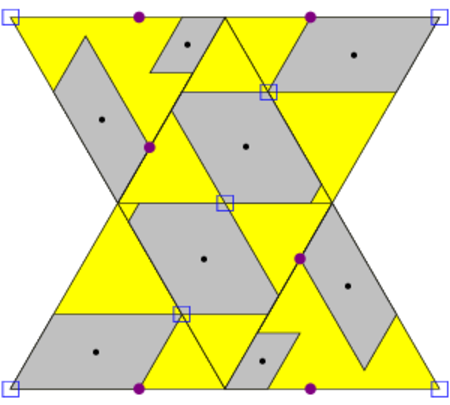
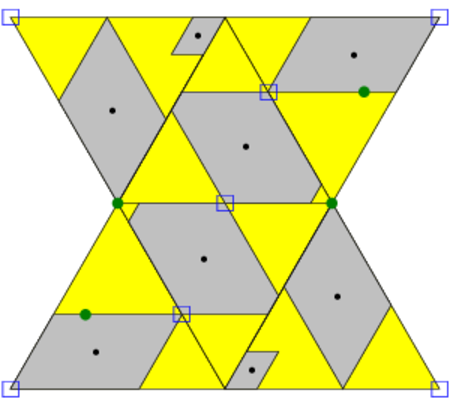
The first set of packings we report on are naturally described as double lattices of bipyramidal dimers. A double lattice is the union of two Bravais lattices related to each other by an inversion operation about some point. In [KK90], Kuperberg and Kuperberg used the idea of a double lattice in the Euclidean plane to show that any planar convex body can be packed in an arrangement with a packing fraction no smaller than $\sqrt{3}/2$. We naturally extend the idea of the double lattice to the three-dimensional Euclidean space. The repeating unit of one constituent lattice is a bipyramidal dimer: two regular tetrahedra sharing a common face. Two of these dimers with mutually-inverted orientation --- a Kuper-pair --- form the repeating unit of the double lattice, which thus has four tetrahedra of distinct orientations. We state the existence of the packings as Theorem 1.
Theorem 1. There exists a one-parameter family of packings of regular tetrahedra, each having packing fraction $110/117$. These packings are periodic, with each unit cell of the lattice containing two bipyramidal dimers. The group of isometries leaving each packing invariant is a crystallographic space group of type $C2/c$ (following the classification and notation of [Mer92]) and acts transitively on the individual tetrahedra of the packing.
Proof. We construct each packing by acting on a single regular tetrahedron with a group of isometries. For a coordinate basis we use three pair-wise orthogonal vectors $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$, of norms $|\mathbf{a}|=2\sqrt{7}/5$, $|\mathbf{b}|=\sqrt{3}/2$, and $|\mathbf{c}|=13\sqrt{3/14}/5$. The initial tetrahedron $T_0=\mathrm{conv} \{\mathbf{r}_i \mid i=1,2,3,4\}$ is the convex hull of four vertices whose coordinates are given in Table 1; it is a regular tetrahedron of unit edge length. The group of isometries is the group of crystallographic type $C2/c$ generated by the translations $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{d}_x=\frac{1}{2}\mathbf{b}+\frac{1}{2}\mathbf{c}+x\mathbf{a}$ ($29/56\le x\le9/14$), by the inversion about the point $0$, and by the rotation by 180 degrees about the axis $\{\frac{1}{4}\mathbf{a}+t\mathbf{b} \mid t \in \mathbb{R}\}$ [Mer92]. This space group has a point group of order 4 and its translations generate a centered monoclinic point lattice. The construction is summarized in Table 1.
| fundamental tetrahedron | $T_0=\mathrm{conv} \{\mathbf{r}_i \mid i=1,2,3,4\}$ $\mathbf{r}_{1}=\frac{27}{28}\mathbf{a}-\frac{7}{30}\mathbf{b}+\frac{10}{39}\mathbf{c}$ $\mathbf{r}_{2}=\frac{1}{4}\mathbf{a}-\frac{9}{10}\mathbf{b}$ $\mathbf{r}_{3}=\frac{1}{14}\mathbf{a}+\frac{1}{10}\mathbf{b}+\frac{5}{13}\mathbf{c}$ $\mathbf{r}_{4}=\frac{3}{7}\mathbf{a}+\frac{1}{10}\mathbf{b}-\frac{5}{13}\mathbf{c}$ |
| other tetrahedra in the unit cell | $T_1=R_2(T_0)=\mathrm{conv} \{\frac{2}{3}(\mathbf{r}_2+\mathbf{r}_3+\mathbf{r}_4)-\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3,\mathbf{r}_4\}$ $T_2=I(T_0)=-T_0$ $T_3=I(T_1)=-T_1$ |
| space group generators | translations by $\mathbf{a}$, $\mathbf{b}$, $\mathbf{d}_x=\frac{1}{2}\mathbf{b}+\frac{1}{2}\mathbf{c}+x\mathbf{a}$ $I=$ inversion about $0$ $R_2=$ two-fold rotation about $\{\frac{1}{4}\mathbf{a}+t\mathbf{b} \mid t \in \mathbb{R}\}$ |
| packing fraction | $100/117$ |
| coordinate basis for which tetrahedra are regular with unit edge length | $\mathbf{a}=(2\sqrt{7}/5,0,0)$ $\mathbf{b}=(0,\sqrt{3}/2,0)$ $\mathbf{c}=(0,0,13\sqrt{3/14}/5)$ |
By construction, each tetrahedron in the packing is the image of $T_0$ under an isometry in the group. We have immediately then that all tetrahedra are congruent with $T_0$, that the packing is invariant under the action of the group, and that the group acts transitively on individual tetrahedra. As the tetrahedra divide into four orbits of the lattice translations, the packing fraction is given by $$\phi=\frac{4 \mathrm{vol}(T_0)}{|\det([\mathbf{a},\mathbf{b},\mathbf{d}_x])|} =\frac{4 (\sqrt{2}/12)}{|\mathbf{a}||\mathbf{b}||\mathbf{c}|/2} =\frac{100}{117}$$
All that is left then to prove the theorem is to verify that the arrangement of tetrahedra thus constructed is indeed a packing. As the packing is transitive (in the sense that its symmetry group acts transitively on the constituent tetrahedra), it is enough to check that one tetrahedron, $T_0$, does not overlap any other tetrahedron. By means of a closest-lattice-point algorithm such as the one in [AEVZ02], we generate a list of all tetrahedra whose centroid is, for any $29/56\le x\le9/14$, at a distance less than $\sqrt{3/2}$ from the centroid of $T_0$. There are 46 such tetrahedra. All other tetrahedra have circumspheres which do not intersect the circumsphere of $T_0$, and therefore they do not intersect $T_0$. For each tetrahedron in the list we can establish the existence of a separating plane separating it from $T_0$. Two tetrahedra have no overlap if and only if they are separated by a plane, and moreover, such a plane always exists which passes through three of the eight vertices of the two tetrahedra. By exhaustively verifying that one of the finitely many planes that pass through three of the vertices separates the two tetrahedra, we establish that each tetrahedron in the list can be separated from $T_0$. ☐
Note that the above construction, which uses a specific orthogonal coordinate basis $\{\mathbf{a},\mathbf{b},\mathbf{c}\}$, is a special case of a general family of packings of non-regular tetrahedra that can be obtained using the same construction, but with a general monoclinic coordinate basis ($\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{c}=0$). Each of these more general packings is an image of a packing in the original family under an affine map from a three-parameter family (not counting pure dilation). As the lack of overlap between tetrahedra and the packing fraction are both affine-invariant, these are also transitive packings of the same packing fraction.
By the construction of the double lattice, there is an inversion center that sends one lattice of dimers into the other. Note that a lattice translation composed with an inversion about a point corresponds to an inversion about a point related to the original inversion center by half the lattice vector. It follows then that in any primitive unit cell of the lattice, there are eight such inversion centers. These eight inversion centers form the vertices of a parallelepiped one-eighth the volume of the primitive unit cell of the lattice. This parallelepiped is the equivalent of the ``extensive parallelogram'' described in [KK90] whose vertices are the inversion points that generate the double lattice. As in [KK90], the parallelepiped is inscribed in the body being packed --- the bipyramidal dimer in our case.
An interesting feature of the packing is the presence of the free parameter $x$. The effect of a change in $x$ is to slide fixed layers of the packing relative one another along the $\mathbf{a}$-direction. These layers are the layer generated by the translations $\mathbf{a}$ and $\mathbf{b}$ from the four tetrahedra of the primitive unit cell and the layers parallel to it. The construction yields a valid packing when the small protrusions in one layer are staggered to fit into small gaps in the neighboring layer, which is the case for all $29/56\le x\le9/14 \pmod{1}$. Within this range, each layer can slide against the neighboring layer without changing the spacing between the two or creating collisions. It is possible then to obtain equally dense, non-transitive packings by staggering consecutive layers arbitrarily within the allowed range.
We describe next the contacts formed by each dimer in the packing, and they are illustrated in Figures 1 and 2. Each of the eight vertices of the inscribed parallelepiped corresponds to the center of a face-face contact between bipyramids of opposite orientations, accounting for all contacts between oppositely-oriented bipyramids. Four of these contacts are within one layer and four of them are with the layers above and below. The contacts formed between like-oriented bipyramids vary with the parameter $x$: for all values of $x$ there are two edge-edge contacts, a vertex-edge contact and an edge-vertex contact (all of these contacts occur on two-fold axes and are within one layer); for $x=29/56$ there are four additional edge-edge contacts with dimers in neighboring layers (which turn into overlaps for $x<29/56$); and for $x=9/14$ there are instead two vertex-face contacts and two face-vertex contacts with dimers in neighboring layers (which again turn into overlaps for $x>9/14$). Thus, each dimer makes respectively twelve, sixteen, or sixteen contacts in the three cases, and correspondingly, each tetrahedron makes eight, ten, or eleven contacts.
Our numerical search also yielded a packing with two tetrahedra per repeating unit, which we could identify as a simple double lattice (that is a double lattice of tetrahedra, not of dimers) with packing fraction $\frac{139+40\sqrt{10}}{369}\approx0.7194$. We present therefore a second theorem.
Theorem 2. There exists a packing of regular tetrahedra having packing fraction $\frac{139+40\sqrt{10}}{369}$. This packing is periodic, with each unit cell of the lattice containing two tetrahedra. The group of isometries leaving the packing invariant is a crystallographic space group of type $P\bar{1}$ and acts transitively on the individual tetrahedra of the packing.
| fundamental tetrahedron | $T_0=\mathrm{conv} \{\mathbf{r}_i \mid i=1,2,3,4\}$ $\mathbf{r}_{1}=[(433-86\sqrt{10})\mathbf{a}+(611-133\sqrt{10})\mathbf{b}+(188-22\sqrt{10})\mathbf{c}]/246$ $\mathbf{r}_{2}=[(111-30\sqrt{10})\mathbf{a}+(93-75\sqrt{10})\mathbf{b}+(-66-42\sqrt{10})\mathbf{c}]/246$ $\mathbf{r}_{3}=[(-85-28\sqrt{10})\mathbf{a}+(13-29\sqrt{10})\mathbf{b}+(4+10\sqrt{10})\mathbf{c}]/246$ $\mathbf{r}_{4}=[(179-106\sqrt{10})\mathbf{a}+(427-101\sqrt{10})\mathbf{b}+(-20-50\sqrt{10})\mathbf{c}]/246$ |
| other tetrahedron in the unit cell | $T_1=I(T_0)=-T_0$ |
| space group generators | translations by $\mathbf{a}$, $\mathbf{b}$, $\mathbf{c}$ $I=$ inversion about $0$ |
| packing fraction | $(139+40\sqrt{10})/369$ |
| coordinate basis for which tetrahedra are regular with unit edge | $\mathbf{a}=(1,-(13-4\sqrt{10})/3,0)$ $\mathbf{b}=(-(4-\sqrt{10})/3,3-\sqrt{10},-1)$ $\mathbf{c}=(3-\sqrt{10},1,(4-\sqrt{10})/3)$ |
The proof of this theorem proceeds equivalently to the proof of Theorem 1. The vertices of the initial tetrahedron $T_0$ are given in Table 2 in terms of a triclinic coordinate basis which is also given in Table 2. The group of isometries we use to construct the packing is generated by translation by the three vectors $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ and by inversion about the origin. This is a space group of crystallographic type $P\bar{1}$, with a point group of order 2 and a triclinic lattice [Mer92]. Figure 3 shows a portion of the packing.
The simple-double-lattice packing again has eight inversion centers per primitive cell at the vertices of a parallelepiped. However, in this case only five of the vertices are on the surface of the tetrahedron. Each tetrahedron in the packing is in contact with nineteen others.
In Table 3, we compare the packings presented here to other studied packings of regular tetrahedra. Both packings are denser than the densest previously-reported transitive packing, a double lattice presented by Conway and Torquato (which we call the "warp-and-weft" packing due to the interweaving arrangement of its tetrahedra) [CT06], and the dimer double lattice is denser than any previously-reported packing.
| Name | $\phi$ | $N$ | $\bar{Z}$ | Transitive |
| Optimal lattice [Hoy70] | $18/49\approx0.3673$ | $1$ | $14$ | Yes |
| Warp and weft [CT06] | $2/3\approx0.6666$ | $2$ | $10$ | Yes |
| Welsh [CT06] | $17/24\approx0.7083$ | $34$ | $25.9$ | No |
| Simple double lattice | $\frac{139+40\sqrt{10}}{369}\approx0.7194$ | $2$ | $19$ | Yes |
| Wagon wheels [Chen08] | $0.7786$ | $18$ | $7.1$ | No |
| Compressed wagon wheels [TY09a] | $0.7820$ | $72$ | $7.6$ | No |
| Disordered wagon wheels [TY09b] | $0.8226$ | $314$ | $7.4$ | No |
| Quasicrystal approximant [HEK09] | $0.8503$ | $656$ | No | |
| Dimer double lattice | $100/117\approx0.8547$ | $4$ | $8$ to $11$ | Yes |
The results presented go against the recent trend of ever-growing repeating units in densest-known packings and demonstrate that a large repeating unit is not a necessary property of a dense packing of regular tetrahedra. It is curious that previous simulations, utilizing a more physical search dynamic [TY09a,TY09b,HEK09], yielded dense packings that were either disordered, had quasicrytalline order, or had crystalline order characterized by a very large repeating unit, and were not able to find the denser class of structures presented here, (reminiscent perhaps of Kurt Vonnegut's ice-nine, a fictional phase of water that is more stable, but kinetically unreachable).
Our results yield the surprising situation wherein the densest-known packing of icosahedra is now sparser than the corresponding packing of tetrahedra, a solid which just four years ago was a prime candidate for a counterexample of a conjecture by Ulam that the sphere is the sparsest-packing convex solid [CT06]. As the packing can be generally extended to any tetrahedron in a three-parameter family generated by deformations of the monoclinic coordinate basis, if any tetrahedron provides a counterexample of Ulam's conjecture, it is not a tetrahedron of that family.
The regular tetrahedron is no longer outcast, as it long was, from the respectable family of convex polyhedra whose largest-achieved packing density is realized by a transitive arrangement. While there are some convex solids whose maximum packing density clearly cannot be achieved by a transitive arrangement (the convex Schmitt-Conway-Danzer polyhedron can tile space, but only in aperiodic and non-transitive ways [Dan94]), the majority of regular and semi-regular polyhedra have been to-date packed most densely in transitive packings [TY09a]. Whether this situation is accidental, the result of bias favoring the discovery of transitive packings, or a more fundamental property governing the packing of a certain class of solids is still an open question.
This work was supported by grant NSF-DMR-0426568.