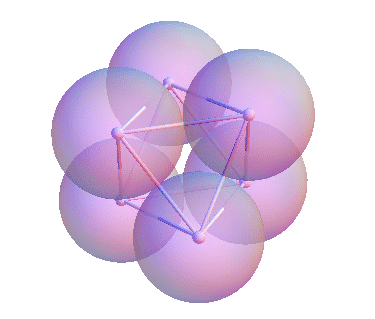The Free Energy of Sticky Sphere Clusters

|
Yoav Kallus and Miranda Holmes-Cerfon APS March Meeting |
Colloidal particles with short range interactions
|
|
 The sticky sphere limit:
The sticky sphere limit:E➞∞, ϵ➞0 |
Energy landscape of a system of sticky spheres
|
Continuous potential
|
$U = -(\text{# of bonds})E$
|
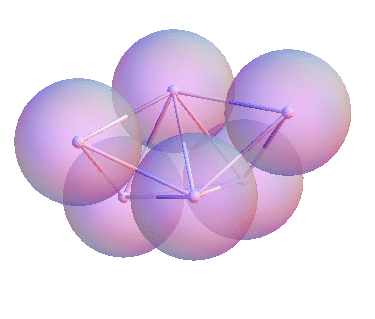
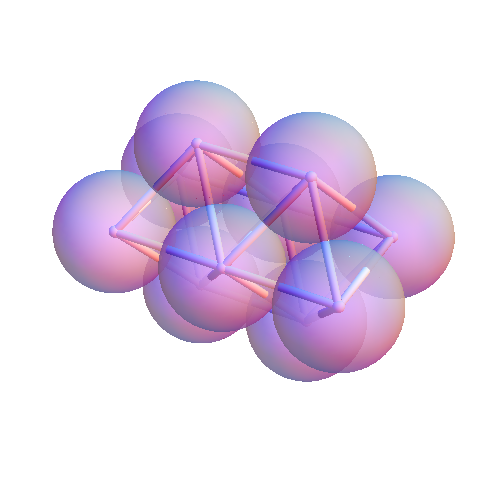
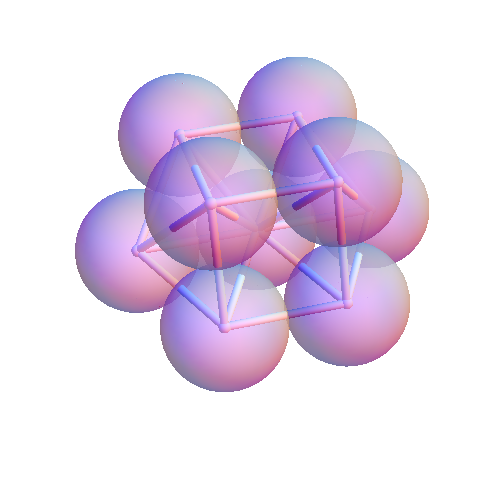
Rigid Clusters and Energy Minima
|
|
|
Cluster Chemistry

Meng, G., Arkus, N., Brenner, M. P., &
Manoharan, V. N., Science (2010)
Cluster Chemistry
|
|
|
$\displaystyle{Z_i = \int_{\mathcal{N}_i\subseteq \mathbb{R}^{3N}} e^{-\beta U(\mathbf{r})}\mathrm{d}^{3N}\mathbf{r}\qquad\qquad Z_2 \approx 20 Z_1}$
Entropic contributions
|
$Z_\mathrm{rot} = e^{S_\mathrm{rot}} = (\det I)^{1/2}/\sigma$ |
$Z_\mathrm{vib} = e^{S_\mathrm{vib}} = \prod_{a=1}^{3N-6} (\beta k_a)^{-1/2}$ |
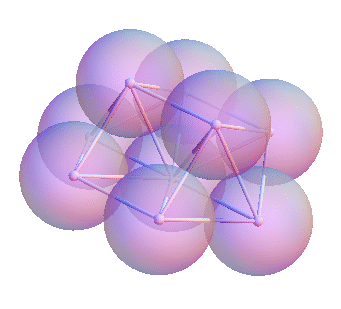
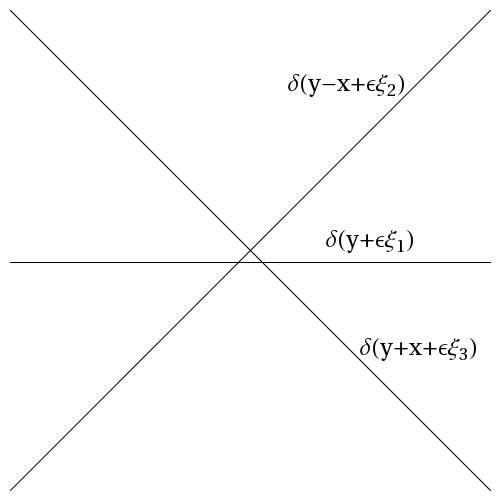
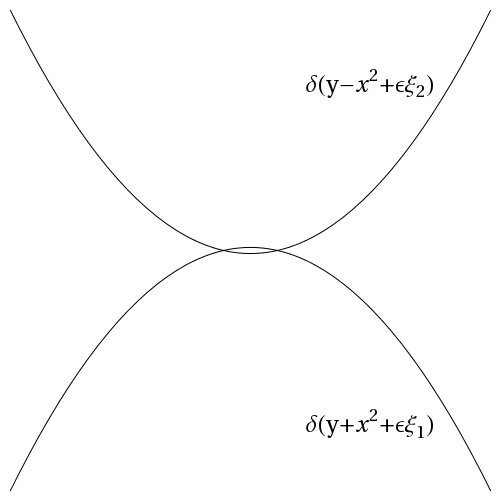
$Z_\text{vib} \to \infty$
Asymptotically leading term
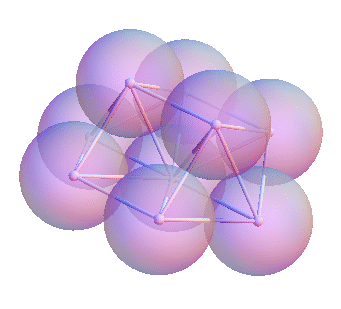
$Z_i ~\propto~ \alpha^{f} e^{\beta E B} z_i + O(\cdots)$
$\alpha = \left[d^2 \beta V''(d) \right]^{1/4}$, $f=$ # of flexes, $B=$ # of bonds, $z_i =$ geometric factor, independent
of the potential
N=9 comparison with simulations
$P_1 = Z_1/\sum_{i=1}^{52}Z_i \approx \frac{\alpha}{235+\alpha}$
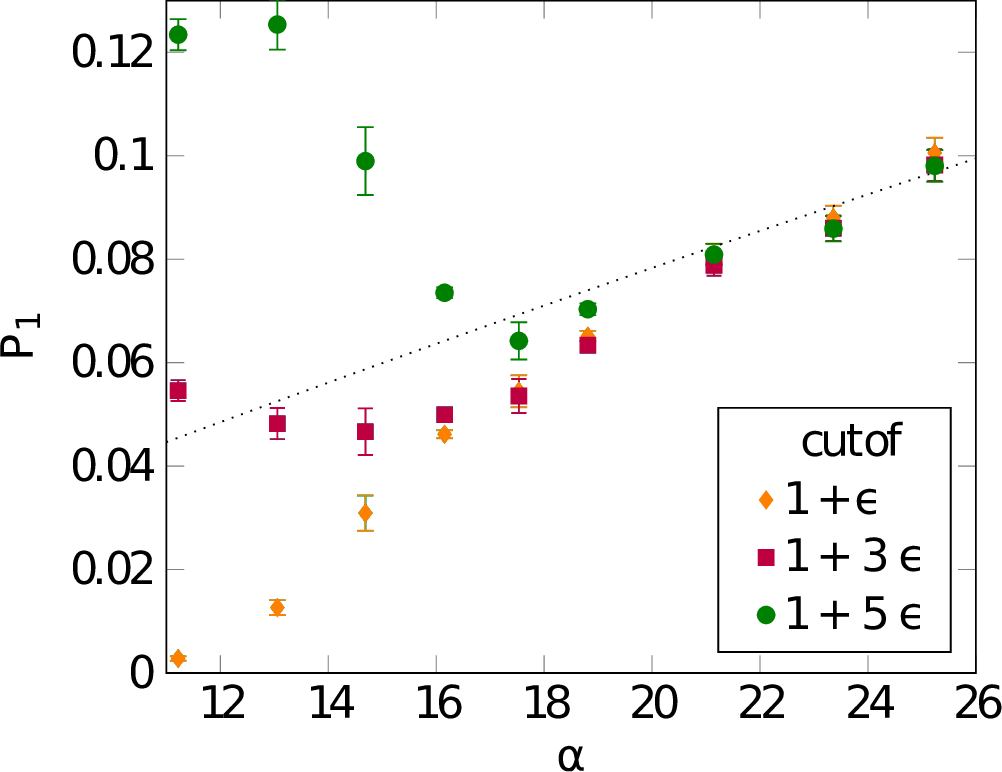
exact only for $\alpha\to 0$ (where $P_1\to 1$), but accurate even when $P_1=.08$.
Baxter's sticky sphere fluid-fluid transition
When $0 < \lim_{1/\epsilon,E\to\infty}\epsilon e^{\beta E} < \infty$,
$e^{-\beta U(\mathbf{r})} \to \prod_{i,j=1}^N (1 + \kappa\delta(r_{ij}-d)) \theta(r_{ij}-d)$
Based on the second order virial coefficient, Baxter (1968) calculated $\kappa_c$ for a gas-liquid transition
|
|
|
Sticky spheres and polydispersity
|
|
|
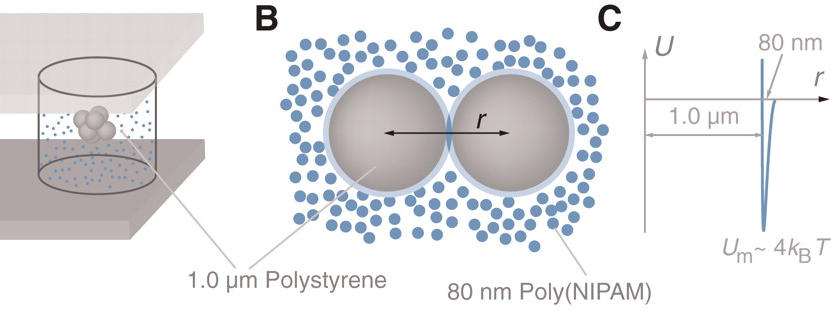 Meng, G., Arkus, N., Brenner, M. P., &
Manoharan, V. N., Science (2010)
Meng, G., Arkus, N., Brenner, M. P., &
Manoharan, V. N., Science (2010)
 Angioletti-Uberti, S., Mognetti, B. M. &
Frenkel, D., Nature Materials (2012)
Angioletti-Uberti, S., Mognetti, B. M. &
Frenkel, D., Nature Materials (2012) Kasha-Katuwe Tent Rocks National Monument
Kasha-Katuwe Tent Rocks National Monument Rio Grande del Norte National Monument
Rio Grande del Norte National Monument Energy minima ≈ rigid bar frameworks
Energy minima ≈ rigid bar frameworks